Algorithms and Complexity Theory
A big topic of theoretical computer science is study how hard is to solve different computational problem. We want to construct efficient algorithms for them, or to prove hardness results showing that such efficient algorithms do no likely exist. By efficient algorithms, we often mean running in polynomial time. To show NP-hardness, we prove that this problem can be used to solve some other NP-hard problem.
For more information and detailed description of our results, see my PhD thesis Extension Properties of Graphs and Structures.
Combinatorial and group theory techniques for the graph isomorphism problem
The graph isomorphism problem asks whether two graphs are the same up to a relabeling called an isomorphism. It is a famous unresolved problem of theoretical computer science, for which it is unlikely it is NP-complete and no polynomial-time algorithm is yet known.
Vaguely speaking, there are two main approaches to attack this problem. Combinatorial techniques are applied to suitable graph classes and use properties such as certain graph decomposition. A prime example of this is the bottom-up dynamic algorithm for graph isomorphism of (rooted) trees. As described in the research project Geometric Representations of Graphs, similar tree decompositions exist for other graph classes including interval graphs and planar graphs. Therefore, their graph isomorphism can be reduced to graph isomorphism of labeled trees. More involved combinatorial algorithms are known for graph isomorphism of bounded genus and bounded treewidth graphs.
The second approach is the use of group theory techniques. As stated in the research project Symmetries and the Graph Isomorphism Problem, automorphism groups of graphs can be used to solve graph isomorphism. Therefore, group theory techniques can be used to compute this group or its certain subgroup. The prime example is the celebrated polynomial-time algorithm of Luks (1982) for bounded degree graphs. No combinatorial algorithm is currently known for these graphs and existence of an FPT algorithm is a major open problem.
In [1], we study the list-restricted version of the graph isomorphism problem; see the research project Symmetries and the Graph Isomorphism Problem for definitions. Lubiw (1981) proved that this problem is NP-complete in general. We study which techniques for graph isomorphism can be modified for the list-restricted problem. We show that aforementioned combinatorial techniques can be straightforwardly modified. On the other hand, the problem remains NP-complete even in the very restricted setting of cubic graphs with bounded sizes of color classes. For both of these restrictions, there are known efficient polynomial-time algorithms solving the graph isomorphism problem. Our research also gives some insight into the general graph isomorphism problem: to solve it efficiently, one has to use some technique which cannot be modified to the list-restricted version.
Topology versus geometry for geometric representations of graphs
In the research project Geometric Representations of Graphs, we have described the partial representation extension problems and we also study other restricted representation problems. For them, we ask whether there exists a representation of an input graph satisfying some additional constraints. For more details, see Section 2.9 of my PhD thesis.
In [2], we study different variant of the partial representation extension problems for chordal graphs as subtree-in-tree graphs and their subclasses. We show the results described in the table below. All hardness results follow a limited space in which we have to pack different components of the graph. Therefore, we can construct suitable instances solving various integer partitioning problems.
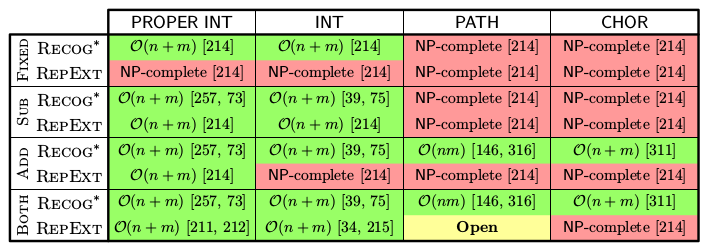 Table of complexities of different variants of the partial
representation extension problems for chordal graphs; see [2] for definitions.
Table of complexities of different variants of the partial
representation extension problems for chordal graphs; see [2] for definitions.In [3], the partial representation extension problems for proper and unit interval graphs are studied. Existence of an extending proper interval representation only only depends on the left-to-right order of endpoints of pre-drawn intervals. On the other hand, we get further geometric constraints for unit interval representations. Both problems are solved in [1], but the quadratic-time algorithm for partial representation extension of unit interval graphs is much more involved. Further, a generalization of partial representation extension called the bounded representation problems are polynomial-time solvable for proper interval graphs [4], but NP-complete for unit interval graphs [3].
Complexity of graph covering
We have described graph covers in the research project Symmetries and the Graph Isomorphism Problem. The computational complexity of general graph covering was mostly studied as locally restricted coloring. For instance, a graph G covers K4 if and only if it is cubic and its vertices can be colored by four colors such that, for each vertex, its neighbors are using all three remaining colors. Therefore, the computational problem H-Cover was studied for a fixed small graph H. When H is not very simple, the problem is almost always NP-complete. In [5], we prove for several small graphs H that the problem H-Cover remains NP-complete even for planar inputs G.
On the other hand, for regular graph covering testing, we do not know any hardness result even when H is a part of the input. In [6,7], we describe a different approach: instead of fixing H, we may restrict the ratio k of sizes of G and H (which is always an integer called fold). When k=1, regular covering testing is precisely the famous graph isomorphism problem. When |H| = 1, it is another unresolved problem called Cayley recognition. (More precisely, a graph G is a Cayley graph if and only if it regularly covers some one-vertex graph H with attached loops and half-edges.) Therefore, we get the k-FoldCover and k-FoldRegularCover problems. It is known that k-FoldCover is NP-complete for k ≥ 3. For k=2, we have 2-FoldCover = 2-FoldRegularCover. The complexity of k-FoldRegularCover is open for all k ≥ 2.
Selected publications
- Pavel Klavík, Dušan Knop, and Peter Zeman: Graph Isomorphism Restricted by Lists. Submitted, 2016. Links: arXiv.
- Pavel Klavík, Jan Kratochvíl, Yota Otachi, and Toshiki Saitoh: Extending Partial Representations of Subclasses of Chordal Graphs. Theoretical Computer Science 576:85-101, 2015. Links: BibTeX, arXiv, journal link.
- Pavel Klavík, Jan Kratochvíl, Yota Otachi, Ignaz Rutter, Toshiki Saitoh, Maria Saumell, and Tomáš Vyskočil: Extending Partial Representations of Proper and Unit Interval Graphs. Algorithmica 77(4):1071-1104, 2017. The conference version appeared in Algorithm Theory, SWAT 2014, volume 8503 of Lecture Notes in Computer Science, pages 253-264, 2014. Links: arXiv, journal link.
- Martin Balko, Pavel Klavík, and Yota Otachi: Bounded Representations of Interval and Proper Interval Graphs. In Algorithms and Computation, ISAAC 2013, volume 8283 of Lecture Notes in Computer Science, pages 535-546, 2013. Links: arXiv, proceedings link.
- Ondřej Bílka, Jozef Jirásek, Pavel Klavík, Martin Tancer, and Jan Volec: On the Complexity of Planar Covering of Small Graphs. In Graph-Theoretic Concepts in Computer Science, WG 2011, volume 6986 of Lecture Notes in Computer Science, pages 83-94, 2011. Links: arXiv, proceedings link.
- Jiří Fiala, Pavel Klavík, Jan Kratochvíl, and Roman Nedela: Algorithmic Aspects of Regular Graph Covers with Applications to Planar Graphs. In Automata, Languages, and Programming, ICALP 2014, volume 8572 of Lecture Notes in Computer Science, pages 489-501, 2014. Links: arXiv, proceedings link.
- Jiří Fiala, Pavel Klavík, Jan Kratochvíl, and Roman Nedela: Algorithmic Aspects of Regular Graphs Covers. The journal version of the algorithmic part of [6], submitted, 2017. Links: arXiv.