Geometric Representations of Graphs

A prime example of geometrically represented graphs is the class of planar graphs. Another examples are classes of intersection graphs in which each vertex is represented by some set and two vertices are adjacent if and only if the corresponding sets intersect. For instance, interval graphs are intersection graphs of closed intervals of the real line.

An interval graph with two different interval representations, with orderings of maximal cliques depicted.

For more information and detailed description of our results, see my PhD thesis Extension Properties of Graphs and Structures.

Structure of all representations

Nicely behaving classes of geometrically represented graphs have the property that all possible geometric representations can be efficiently described and understood. For instance, interval graphs have MPQ-trees of Booth and Lueker (1979), Korte and Möhring (1989) describing all possible interval representations by one tree data structure.

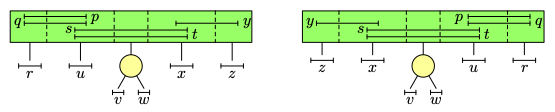Two equivalent MPQ-trees corresponding to two above interval representations.

For planar graphs, decomposition into 3-connected components (which have unique embeddings into the sphere) was pioneered by Mac Lane (1937) and Trakhtenbrot (1958). It was followed by multiple papers and it was recently popularized under the name SPQR trees. In [1], we have described an augmented version of 3-connected decomposition which captures automorphism groups. For description of our results and comparison with previous results, see Chapters 6 and 7 of my PhD thesis. This is related to the research project Symmetries and graph isomorphism.

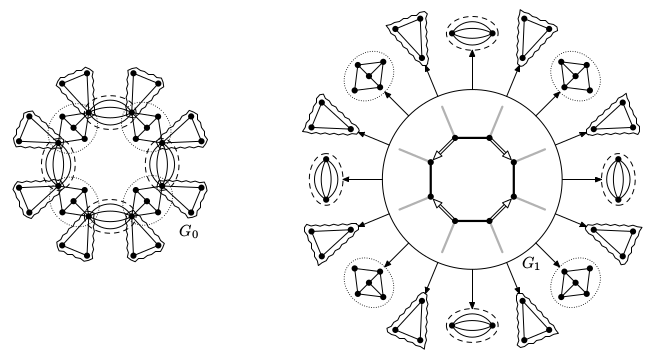On the left, a graph G. On the right, the 3-connected decomposition of G captured by a tree.

The partial representation extension problems

This problem is already from my bachelor's thesis from 2010. Given a graph and a partial intersection representation, we ask whether this partial representation can be extended to a full representation of the input. For instance for interval graphs, some intervals are pre-drawn, fixed by the input, and we ask whether the remaining interval can be added to form the full interval representation.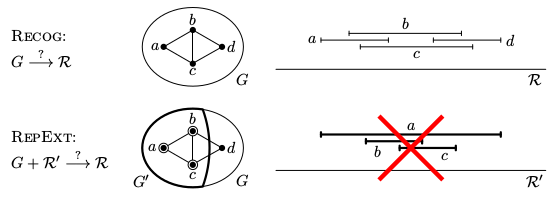

Comparison of the recognition problems (Recog) and of the partial representation extension problems (RepExt). For interval graphs, we prove the following results:

Theorem: [2,4] There exists a linear-time certifying algorithm for the partial representation extension problem of interval graphs. If the answer is "yes", it outputs an extending representation. If the answer is "no", it detects one of the minimal obstructions.

Concerning structural characterizations, we generalize both Fulkerson-Gross and Lekkerkerker-Boland to partially represented interval graphs. In [2], we prove that a partial interval representation is extendible if and only if there exists a consecutive ordering of maximal cliques extending some partial ordering derived from the partial representation. In [4], we characterize minimal obstructions which make a partial interval representation non-extendible. See Chapters 2, 3, and 4 of my PhD thesis. Currently, the complexity of the partial representation extension problems is understood for a variety of classes of intersection graphs. In [3], we describe a linear-time algorithm for proper interval graphs and almost quadratic-time algorithm for unit interval graphs. In [5], we describe a cubic-time algorithm for circle graph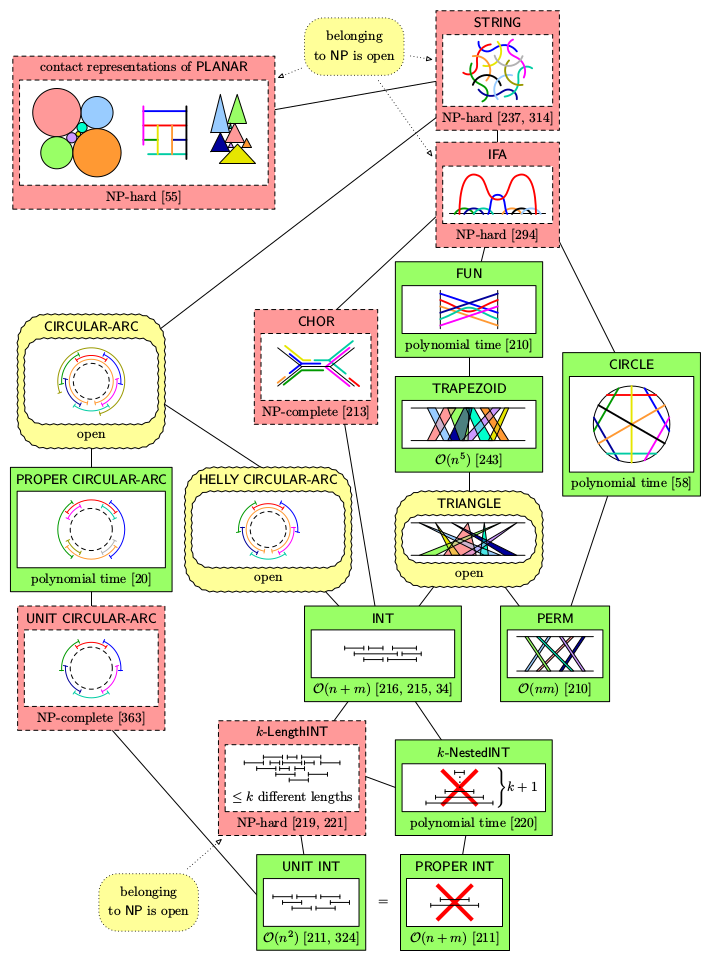s.

Hasse diagram of the main classes of geometrically represented graphs together with the complexity of the partial representation extension problems. For references, see page 57 of my PhD thesis.

Cops and robber on intersection graphs

In [6], we have studied the game of Cops and Robber on intersection graphs. We prove the following results:

Theorem: [6] For every connected string graph, 15 cops are sufficient to catch the robber.

On the other hand, for many basic classes of intersection graphs of disconnected or spacial sets, we prove that the needed number of cops in unbounded.

Selected publications

Jiří Fiala, Pavel Klavík, Jan Kratochvíl, and Roman Nedela:
Algorithmic Aspects of Regular Graph Covers with Applications to Planar Graphs.
In Automata, Languages, and Programming, ICALP 2014, volume 8572 of Lecture Notes in Computer Science, pages 489-501, 2014.
Links: arXiv, proceedings link.
Pavel Klavík, Jan Kratochvíl, Yota Otachi, Toshiki Saitoh, and Tomáš Vyskočil:
Extending Partial Representations of Interval Graphs.
Algorithmica 78(3):945-967, 2017.
The conference version appeared in Theory and Applications of Models of Computation, TAMC 2011, volume 6648 of Lecture Notes in Computer Science, pages 276-285, 2011.
Links: arXiv, journal link.
Pavel Klavík, Jan Kratochvíl, Yota Otachi, Ignaz Rutter, Toshiki Saitoh, Maria Saumell, and Tomáš Vyskočil:
Extending Partial Representations of Proper and Unit Interval Graphs.
Algorithmica 77(4):1071-1104, 2017.
The conference version appeared in Algorithm Theory, SWAT 2014, volume 8503 of Lecture Notes in Computer Science, pages 253-264, 2014.
Links: arXiv, journal link.
Pavel Klavík, and Maria Saumell:
Minimal Obstructions for Partial Representations of Interval Graphs.
Submitted, 2015.
The conference version appeared in Algorithms and Computation, ISAAC 2014, volume 8889 of Lecture Notes in Computer Science, pages 401-413, 2014.
Links: arXiv, proceedings link.
Steve Chaplick, Radoslav Fulek, and Pavel Klavík:
Extending Partial Representations of Circle Graphs.
Submitted, 2015.
The conference version appeared in Graph Drawing, GD 2013, volume 8242 of Lecture Notes in Computer Science, pages 131-142, 2013.
Links: arXiv, proceedings link.
Tomáš Gavenčiak, Przemysław Gordinowicz, Vít Jelínek, Pavel Klavík, and Jan Kratochvíl:
Cops and Robbers on Intersection Graphs.
Submitted, 2016.
The conference versions appeared in Algorithms and Computation, ISAAC 2013, volume 8283 of Lecture Notes in Computer Science, pages 174-184, 2013,
and in Algorithms and Computation, ISAAC 2015, volume 9472 of Lecture Notes in Computer Science, pages 355-366, 2015.
Links: arXiv, proceedings link ISAAC 2013, proceedings link ISAAC 2015.